Números en coma flotante
(13 páginas)
1. Idea básica
1.1. LImitaciones de punto fijo
El punto fijo es repartir los n bits disponibles entre la parte entera y la parte fraccionaria. Pero tiene sus limitaciones. EL balance entre el rango y la precisión es frágil.
- Más bits en la parte fraccionaria: Ganamos precisión. Perdemos rango.
- Más bits en la parte entera: Ganamos rango. Perdemos precisión.
Esto es poco flexible.
2. Punto flotante
Su filosofía es la de hacer que el punto del binario no sea fijo, sino que pueda ir variando.
2,35 x 10⁰ = 0,235 x 10¹ = 0,00235 x 10³
Si tenemos 24,584 x 10⁰
Significando es 24,584 Mantisa es 584 Base es 10 Exponente es 0
- Más bits para mantisa: Ganamos precisión. Perdemos rango.
- Más bits para exponente: Ganamos rango. Perdemos precisión.
3. Notación normalizada
2,35 · 10⁰
- La primera cifra significativa se pone a la izuierda del punto.
- Simplifica el cambio de datos entre unidades funcionales
- Simplifica los algoritmos para la aritmética
- Incrementa la precisión para los números que pueden almacenarse con el mismo número de bits
4. El estandar IEEE 745
Solo guarda la parte fraccionaria. Con esto permite ahorrar un bit.
- Mantisa codificada en magnitud y signo con el signo aparte
- Exponente codificado en exceso z (representación sesgada): 2^(n-1)-1
Teniendo 3 bits en cpl2, el exceso_z sería 3: 011
000: 0 en exz: 011 ( 0)
001: 1 en exc: 100 ( 1)
010: 2 en exz: 101 ( 2)
011: 3 en exz: 110 ( 3)
100: -4 en exz: 111 ( 4)
101: -3 en exz: 000 (-3)
110: -2 en exz: 001 (-2)
111: -1 en exz: 010 (-1)
El numero más pequeño es aquel que tiene la representación binaria en binario puero más pequeño, y el numero mayor es el que tiene en binario puro, la representación mayor
- Incluye símbolos especiales para representar ciertos resultados de operaciones (infinito/NaN)
- Pensado para permitir ordenaciones más rapidas
4.1. Codificación
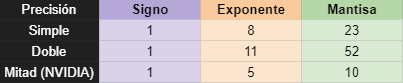
Primero se codifica el bit, luego exponente, y luego la mantisa.

4.2. Números denormalizados
Se usa para el Agotamiento gradual. Sucede que, en el resto de codificaciones 1,0·2^(Emin) = 0
Pero en IEEE 754 se permite lo siguiente
Teniendo 3 bits en cpl2, el exceso_z sería 3: 011
x = 1,234·10^(Emin) en base10 con 4 cifras significativas.
x/10 = 0,123·10^(Emin)
x/100 = 0,012·10^(Emin)
x/1000 = 0,001·10^(Emin)
x/10000 = 0
Solo peremos la precision cuando no hay capacidad para representar el numero. Y gracias al agotamiento gradual podemos cumploer que una resta es 0 si y solo sí los numeros son iguales (x = y ↔ x-y = 0)